Hive UDAF 实战——高性能的用户在线时长聚合函数

agicy2025/10/1大约 17 分钟

Hive UDAF 实战——高性能的用户在线时长聚合函数

本文所探讨和实现的技术方案，源于 2025 年北京邮电大学柠檬微趣奖学金 的一个课题。该课题旨在设计并实现一个自定义 Hive 聚合函数，以高效计算游戏玩家的在线时长，考验了参与者在分布式计算、性能优化及工程实践方面的综合能力。

在游戏数据分析等海量用户行为分析场景中，精确计算用户的「总在线时长」是一项基础且关键的指标。本文将详细阐述如何基于 Apache Hive 框架，设计并实现一个高效的 用户自定义聚合函数（User-Defined Aggregate Functions，UDAF）^[1]，用于解决这一特定业务需求。我们将从一个简单的基准实现出发，剖析其性能瓶颈，并提出一系列递进的优化策略，最终实现性能的显著提升。

项目源码已开源

本文所介绍的基准方案与最终优化方案的完整 Java 源代码以及相关测试脚本，均已托管至 GitHub，仓库地址： https://github.com/agicy/microfun2025-udaf。欢迎查阅、Star 或提出改进意见！

问题描述：计算用户在线时长

我们的目标是统计每个用户一天的总在线时长。给定一系列用户活跃时间点的时间戳（精确到秒），我们定义：如果两个时间点的间隔小于一个预设的阈值（本课题中为 $600$ 秒，即 $10$ 分钟），则认为这两个时间点属于同一个连续的活跃区间。用户的总在线时长即为所有连续活跃区间长度的总和。

例如

某用户一天的活跃时间点为 $2, 3, 99, 1000, 1100, 1101, 9999, 20051, 20651$ 。根据规则，可以将它们划分为三个活跃区间，分别是 $[2, 99]$ 、 $[1000, 1101]$ 和 $[20051, 20651]$ ，从而该用户总在线时长可计算如下。

(99 - 2 + 1) \ \text{秒} + (1101 - 1000 + 1) \ \text{秒} + (20651 - 20051 + 1) \ \text{秒} = 801 \ \text{秒}

在 Hive 中，我们期望通过一个 UDAF $\texttt{get\_online\_duration(timestamps)}$ 来实现这个计算逻辑。

查询用户在线时长的 SQL 语句
SELECT
    userid,
    get_online_duration(active_time)
FROM all_user_active_time
GROUP BY userid;

基准实现及其瓶颈

一个直观的实现思路遵循了聚合函数的基本逻辑。

实现思路

Map 阶段： UDAF 的 $\texttt{iterate}$ 方法接收每个用户的活跃时间点，并将这些时间点添加到一个动态数组中。
Combine / Reduce 阶段： $\texttt{terminatePartial}$ 方法对 Mapper 产出的部分结果发送给 Reducer， $\texttt{merge}$ 方法将收到的不同 Mapper 产出的数组进行合并。
Reduce 阶段： 最终，在 Reducer 节点的 $\texttt{terminate}$ $terminate$ 方法中，对聚合到的包含所有时间点的完整数组执行以下操作：
- 全局排序： 对数组进行排序，时间复杂度为 $\Theta(N \log N)$ ，其中 $N$ 是该用户总的活跃点数量。
- 线性扫描： 遍历排序后的数组，计算相邻时间点的差值，累加有效活跃时长，合并活跃区间。时间复杂度为 $\Theta(N)$ 。

性能瓶颈

这个基准实现虽然逻辑简单，但存在显著的性能问题：

内存压力大： Reducer 需要缓存一个用户的所有时间点数据。对于活跃度极高的用户，这可能导致 内存溢出（Out Of Memory，OOM）。
网络开销高： 从 Map 阶段到 Reduce 阶段需要传输海量的原始时间点数据，这将占用大量的网络带宽。
计算成本高： 全局排序的计算开销较大，尤其是在数据量巨大时，成为计算的主要瓶颈。

性能优化之旅

为了克服上述瓶颈，我们设计了三项递进的优化措施。

优化一：分块算法

问题设定

我们有一个成本函数，其形式为：

\texttt{cost}(B; \alpha, \beta) = \alpha \cdot \frac{N}{B} + \beta \cdot B

其中，数据总量为 $N$ ，块大小为 $B$ 。参数 $\alpha > 1$ 和 $\beta > 1$ 是未知的正常数，分别代表处理一个数据块的成本权重和处理一个块内元素的成本权重。我们的目标是在对 $\alpha$ 和 $\beta$ 没有任何先验知识 的情况下，选择一个最优的块大小 $B$ ，以最小化期望的计算成本。

建立贝叶斯模型

在贝叶斯框架下，我们将未知的 $\alpha$ 和 $\beta$ 视为随机变量。「无先验知识」意味着我们没有理由相信 $\alpha$ 比 $\beta$ 更大或更小，也没有理由认为某个特定的值比其他值更有可能出现。

对称性假设：由于我们对 $\alpha$ 和 $\beta$ 的行为一无所知，最合理的假设是它们是 独立同分布 的。也就是说，它们遵循相同的概率分布，并且相互独立。
$P(\alpha, \beta) = P(\alpha) P(\beta)$
且 $P(\alpha)$ 和 $P(\beta)$ 是相同的函数形式。
定义无信息先验：对于一个正的尺度参数（如 $\alpha$ 和 $\beta$ ），标准的无信息先验是 杰弗里斯先验 ^[2]，其形式为 $P(\theta) \propto \frac{1}{\theta}$ 。这个先验在对数尺度上是均匀的，体现了「尺度不变性」。然而，这是一个 非正常先验，因为它在 $(1, +\infty)$ 上的积分是发散的，这会导致期望值无穷大，使问题无法直接求解。
为了使推导严谨，我们使用一个正常但「模糊」的先验来逼近它。我们假设 $\alpha$ 和 $\beta$ 都分布在某个我们不关心的、足够大的区间 $[1, M]$ 内，其中 $M \to +\infty$ 。在此区间内，我们使用杰弗里斯先验的形式。
因此， $\alpha$ 的先验概率密度函数为：
$P(\alpha) = \begin{cases} \frac{1}{Z \cdot \alpha} & \text{if } 1 \le \alpha \le M \\ 0 & \text{otherwise} \end{cases}$
其中 $Z$ 是归一化常数，有
$Z = \int_{1}^{M} \frac{1}{\alpha} \ \mathrm{d}\alpha = \ln(M).$
对于 $\beta$ 也是如此。

计算期望成本

我们的决策（选择 $B$ ）应该基于最小化期望成本。期望成本 $J(B)$ 是对所有可能的 $\alpha$ 和 $\beta$ 值进行积分：

J(B) = \mathbb{E}_{\alpha, \beta}\left[\texttt{cost}(B; \alpha, \beta)\right] = \iint_{(1, M) \times (1, M)} \left(\alpha \frac{N}{B} + \beta B\right) P(\alpha, \beta) \, \mathrm{d}\alpha \, \mathrm{d}\beta

利用期望的线性性质：
$\begin{aligned} J(B) &= \mathbb{E}\left[\alpha \frac{N}{B} + \beta B\right] \\ &= \mathbb{E}[\alpha] \cdot \frac{N}{B} + \mathbb{E}[\beta] \cdot B \end{aligned}$
计算 $\mathbb{E}[\alpha]$ ：
$\begin{aligned} \mathbb{E}[\alpha] &= \int_{1}^{M} \alpha \cdot P(\alpha) \ \mathrm{d}\alpha \\ &= \int_{1}^{M} \alpha \cdot \frac{1}{\alpha \ln(M)} \ \mathrm{d}\alpha \\ &= \frac{1}{\ln(M)} \int_{1}^{M} 1 \ \mathrm{d}\alpha \\ &= \frac{M-1}{\ln(M)} \end{aligned}$
计算 $\mathbb{E}[\beta]$ ：由于 $\alpha$ 和 $\beta$ 是独立同分布的，它们的期望值相等。
$\mathbb{E}[\beta] = \mathbb{E}[\alpha] = \frac{M-1}{\ln(M)}$
得到期望成本函数 $J(B)$ ：
$J(B) = \frac{M-1}{\ln(M)} \cdot \frac{N}{B} + \frac{M-1}{\ln(M)} \cdot B = \frac{M-1}{\ln(M)} \left( \frac{N}{B} + B \right)$

最小化期望成本

为了找到最优的块大小 $B$ ，我们对 $J(B)$ 求关于 $B$ 的一阶导数和二阶导数。

对 $J(B)$ 求导：
$\begin{aligned} \frac{\mathrm{d}J}{\mathrm{d}B} &= \frac{\mathrm{d}}{\mathrm{d}B} \left[ \frac{M-1}{\ln(M)} \left( N B^{-1} + B \right) \right] \\ &= \frac{M-1}{\ln(M)} \cdot \frac{\mathrm{d}}{\mathrm{d}B} \left( N B^{-1} + B \right) \\ &= \frac{M-1}{\ln(M)} \left( -N B^{-2} + 1 \right) \\ &= \frac{M-1}{\ln(M)} \left( 1 - \frac{N}{B^2} \right) \end{aligned}$ $\begin{aligned} \frac{\mathrm{d}^2J}{\mathrm{d}B^2} &= \frac{\mathrm{d}^2}{\mathrm{d}B^2} \left[ \frac{M-1}{\ln(M)} \left( N B^{-1} + B \right) \right] \\ &= \frac{M-1}{\ln(M)} \cdot \frac{\mathrm{d}^2}{\mathrm{d}B^2} \left( N B^{-1} + B \right) \\ &= \frac{M-1}{\ln(M)} \left( 2 N B^{-3} + 0 \right) \\ &= \frac{M-1}{\ln(M)} \left( \frac{2N}{B^3} \right) \end{aligned}$
令导数为零求解 $B$ ：
$\frac{M-1}{\ln(M)} \left( 1 - \frac{N}{B^2} \right) = 0$
由于 $M > 1$ ，系数项 $\frac{M-1}{\ln(M)}$ 不为零，因此必须有：
$\begin{aligned} 1 - \frac{N}{B^2} &= 0 \\ 1 &= \frac{N}{B^2} \\ B^2 &= N \end{aligned}$
因为块大小 $B$ 必须为正数，所以我们得到最优解：
$B_{\text{opt}} = \sqrt{N}$
在此处 $J(B)$ 关于 $B$ 的二阶导数
$\frac{M-1}{\ln(M)} \left( \frac{2N}{B^3} \right) > 0$
故 $J(B)$ 在 $B = \sqrt{N}$ 处达到最小值。

结论

通过运用贝叶斯思想，我们将未知的成本系数 $\alpha$ 和 $\beta$ 建模为服从对称的、无信息先验分布的随机变量。通过严谨的微积分推导，我们计算了期望成本函数，并通过最小化该期望成本，最终确定了最优的块大小为 $B = \sqrt{N}$ 。这个结果的优美之处在于，它与我们选择的先验分布的具体范围 $[1, M]$ 无关，显示了其普适性和鲁棒性。

因此，在算法设计时，我们一旦注意到了存在的已知线性算法和算术平方根大小的分块策略，就可以尝试通过分块方法来优化算法的性能。

算法原理

我们注意到，时间间隔阈值为 $600$ 秒，约为时间戳数据范围 $86400$ 的算数平方根（ $\sqrt{86400} \approx 293.93876913$ ）的两倍。利用这个业务特性，我们可以将一天的时间域划分为 $144$ 个长度为 $600$ 秒的连续块。

该分块策略具备以下优良性质：

性质一：块内任意两点构成活跃区间。 块内任意两个时间点的最大距离为 $599$ 秒，小于阈值 $600$ 秒。因此，它们必然属于同一个活跃区间。
- 推论： 对于每个块，我们无需存储所有时间点，只需记录该块内出现的最早时间（ $\texttt{min\_offset}$ ）和最晚时间（ $\texttt{max\_offset}$ ）相对于块起始点的偏移量即可。块内的活跃时长即为 $\texttt{max\_offset} - \texttt{min\_offset} + 1$ 。
性质二：非相邻块的任意两点不能直接构成活跃区间。 处于非相邻块（如第 $i$ 块和第 $i + 2$ 块）的任意两个时间点，其最小距离也大于 $600$ 秒。
- 推论： 在最终统计时，我们只需考虑块内的活跃时长以及相邻两个块之间的连接关系。

这个优化将最终的计算复杂度从 $\Theta \left( N \log N \right)$ 降低到 $\Theta (k)$ ，其中 $k$ 为块的数量（ $k=144$ ），与原始数据量 $N$ 无关，实现了质的飞跃。

UDAF 实现

$\texttt{iterate(timestamp)}$ ：对输入的时间戳 $\texttt{timestamp}$ ，计算其所属的 $\texttt{block\_id}$ 和块内偏移量 $\texttt{offset}$ ，并更新对应块的 $\texttt{min\_offset}$ 和 $\texttt{max\_offset}$ 。
$\texttt{terminatePartial()}$ ：输出一个包含 $144$ 个块的 $\left[ \texttt{min\_offset}, \texttt{max\_offset} \right]$ 信息的数据结构。
$\texttt{merge(partial\_data)}$ ：遍历 $144$ 个块，用接收到的部分聚合数据更新当前聚合结果中每个块的 $\texttt{min\_offset}$ 和 $\texttt{max\_offset}$ 。
$\texttt{terminate()}$ ：线性遍历 $144$ 个块的最终聚合结果，累加每个块内的活跃时长，并检查相邻块之间是否可以连接（即后一块的 $\texttt{min\_offset}$ 与前一块的 $\texttt{max\_offset}$ 对应的全局时间差小于等于 $600$ 秒），累加跨块连接的活跃时长，得出最终结果。

优化二：利用 BitSet 优化稀疏数据网络传输

动机

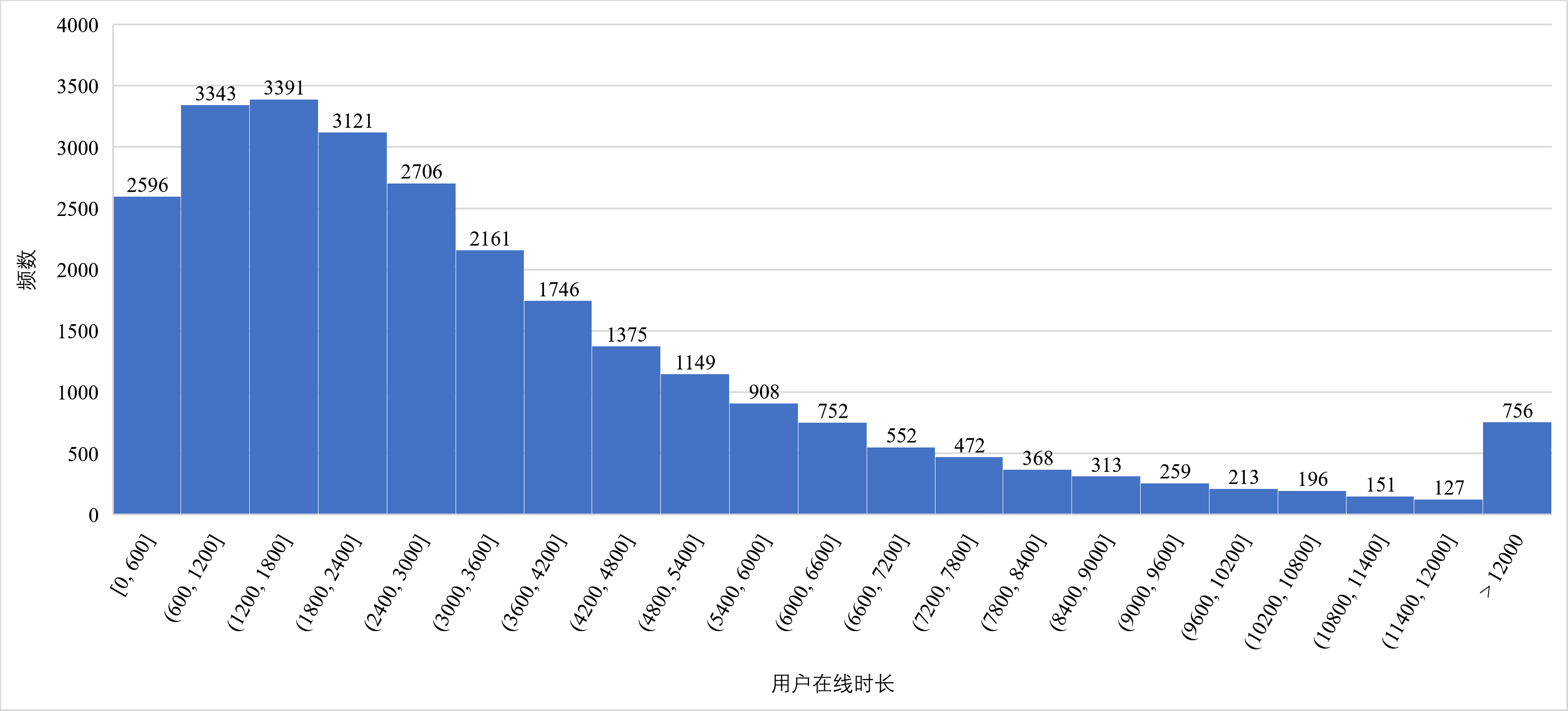
通过分析测试数据，我们发现大量用户的在线行为呈现高度稀疏性。

上图展示了用户活跃时长的分布情况，通过分析给定测试数据，我们发现，在 $26655$ 名用户中，在线时长不超过 $6000$ 秒的用户共 $22496$ 名，占比约 $84.40 \%$ ，即 $84.40 \%$ 的用户活跃点仅分布在少数（约 $10$ 个）块中，数据呈现高度的稀疏性。而优化一中，无论块内有无数据，都会传输 $144$ 个块的信息，造成了网络带宽大约 $\frac{144}{10} = 14.4$ 倍的浪费。

实现

我们引入 $\texttt{java.util.BitSet}$ ^[3] 来标记存在活跃时间点的块。 $\texttt{BitSet}$ 是一种空间效率极高的数据结构，非常适合表示稀疏的布尔值集合。

在聚合状态中增加一个位数为 $288$ 的 $\texttt{BitSet}$ ，其中第 $2 i$ 位表示第 $i$ 个块是否有数据，第 $2 i + 1$ 位表示第 $i$ 个块是否第 $i + 1$ 个块有连接，下标为 $287$ 的位留作哨兵。
$\texttt{iterate}$ 方法在更新块的数据时，同时在 $\texttt{BitSet}$ 中将对应块的标志位设为 $1$ 。
$\texttt{terminatePartial}$ 和 $\texttt{merge}$ 方法在序列化和反序列化时，先传输 $\texttt{BitSet}$ ，然后仅传输 $\texttt{BitSet}$ 中被标记为 $1$ 的那些块的数据。

这项优化极大地减少了在 Map-Combine-Reduce 各阶段之间传输的数据量，尤其对绝大多数非重度活跃用户效果显著。

优化三：ByteBuffer 手动序列化优化 I/O

动机

经过优化二，聚合数据结构变得紧凑且格式固定。此时，Java 默认的序列化机制由于需要写入类元数据等额外信息，显得较为低效。我们需要一种更底层、性能更佳的序列化方案。

实现

我们采用 $\texttt{java.nio.ByteBuffer}$ ^[4] 进行手动序列化和反序列化，实现对字节的直接操作。

序列化：
1. 根据 $\texttt{BitSet}$ 精确计算出存在的段数 $\texttt{count}$ ，从而计算所需字节数 $\texttt{size} = \texttt{sizeof}(\texttt{BitSet}) + \texttt{count} \times \texttt{sizeof}(\texttt{Short}) \times 2$ 。
2. 创建一个恰好大小的 $\texttt{ByteBuffer}$ 。
3. 将 $\texttt{BitSet}$ 转换为 $\texttt{long}$ 数组后写入 Buffer，再依次写入所有活跃块的偏移量。
反序列化：
1. 按写入顺序依次读出 $\texttt{long}$ 数组并恢复 $\texttt{BitSet}$ 。
2. 然后根据 $\texttt{BitSet}$ 读取相应数量的偏移量。

通过使用 $\texttt{ByteBuffer}$ ，我们避免了 Java 序列化的额外开销，直接操作字节，获得了更高的 I/O 性能。

程序测试与性能分析

给定环境下的性能对比

我们采用 $\texttt{k-best}$ 方法 ^[5] 对基准实现和最终优化版本进行了性能测试，其中测量参数 $k=3$ ， $N=20$ ， $\varepsilon=0.05$ ，数据处理的核心代码如下。

k-best 方法的核心代码
"""
This module provides a utility function, `k_best`, designed to find a stable
minimum measurement from a stream of asynchronous inputs. It uses a k-best
selection strategy combined with a relative error criterion to determine
when a sufficiently "good" minimum has been identified.

The primary function `k_best` continuously takes measurements and maintains
a set of the `k` smallest measurements seen so far, while also tracking the
absolute minimum measurement. It converges when the relative error between
the `k`-th smallest measurement and the overall minimum falls below a specified
epsilon threshold.
"""

__all__: list[str] = ["k_best"]

import heapq
from typing import Awaitable, Callable


def __relative_error(
    measurement: float,
    reference: float,
) -> float:
    """
    Calculates the absolute relative error between a measurement and a reference value.

    Args:
        measurement: The measured value.
        reference: The reference value.

    Returns:
        The absolute relative error.
    """

    return abs(measurement - reference) / reference


async def k_best(
    k: int,
    n: int,
    epsilon: float,
    input_function: Callable[[], Awaitable[float]],
) -> float:
    """
    Finds the minimum measurement such that the relative error between the
    k-th largest measurement (among those currently considered 'best') and
    the overall minimum measurement encountered so far is within `epsilon`.

    This function continuously samples `n` measurements from `input_function`.
    It maintains the `k` largest measurements seen so far using a max-heap
    (simulated with a min-heap by negating values). Simultaneously, it tracks
    the absolute minimum measurement observed. The process terminates and
    returns the overall minimum measurement when the relative error condition is met.

    Args:
        k: The number of "best" (largest) measurements to consider for the error check.
           Must be greater than 0.
        n: The maximum number of measurements to take. Must be greater than 0
           and greater than or equal to k.
        epsilon: The acceptable relative error threshold. Must be greater than 0.
        input_function: An asynchronous callable that returns a new float measurement.
                        Each measurement must be greater than 0.

    Returns:
        The overall minimum measurement encountered when the convergence criterion is met.

    Raises:
        ValueError:
            - If `k`, `n`, or `epsilon` are not valid (e.g., non-positive, or n < k).
            - If any `measurement` returned by `input_function` is not greater than 0.
            - If `n` measurements are processed and the k-best measurements (satisfying
              the epsilon condition) are not found.
    """

    if k <= 0:
        raise ValueError(f"k must be greater than 0, got {k}")
    if n <= 0 or n < k:
        raise ValueError(
            f"n must be greater than 0 and greater than or equal to k, got {n}"
        )
    if epsilon <= 0:
        raise ValueError(f"epsilon must be greater than 0, got {epsilon}")

    measurement_count: int = 0
    minimum: float = float("inf")
    # Use a min-heap to store negated measurements. This effectively simulates a max-heap
    # for the actual measurements, allowing us to easily retrieve the k largest values.
    # The heap will always contain at most 'k' elements, representing the k largest
    # measurements encountered that are still relevant.
    heap: list[float] = []

    while measurement_count < n:
        # Fetch a new measurement value
        measurement: float = await input_function()
        measurement_count += 1

        if measurement <= 0:
            raise ValueError(f"measurement must be greater than 0, got {measurement}")

        # Update the overall minimum measurement encountered
        minimum = min(minimum, measurement)

        # Push the negated measurement onto the min-heap.
        # This way, the smallest element in the heap corresponds to the
        # largest actual measurement (because it's the smallest negative).
        heapq.heappush(heap, -measurement)

        # If the heap size exceeds k, remove the smallest element.
        # For our negated values, this means removing the element that corresponds
        # to the largest actual measurement, thus keeping only the k smallest.
        if len(heap) > k:
            heapq.heappop(heap)

        # Once we have collected k measurements in the heap, we can perform the check.
        if len(heap) == k:
            # The top of the min-heap (smallest element) is the negative of the
            # k-th largest measurement. Negate it to get the actual largest value.
            # This is the 'maximum' of our current k-best set.
            maximum: float = -heap[0]

            # Check if the relative error between the current largest measurement
            # and the overall minimum measurement is within the acceptable epsilon.
            if (
                __relative_error(
                    measurement=maximum,
                    reference=minimum,
                )
                <= epsilon
            ):
                # If the condition is met, return the overall minimum measurement.
                return minimum

    # If n measurements are processed and the k-best condition is not met, raise an error.
    raise ValueError(
        f"k-best measurements not found within {n} attempts. Minimum measurement found is {minimum}"
    )

下表中的测试结果表明，在处理相同数据集时，优化后的 UDAF 相较于基准实现，在处理时间方面有较大的缩减。

项目	基准实现（秒）	优化后实现（秒）
最终得分 (平均值)	$21.66$	$12.40$
性能优化比	-	$\approx 42.75 \%$

测试结果表明，优化后的 UDAF 相较于基准实现，运行时间平均减少了约 $42.75 \%$ ，性能提升显著。

自定义压力测试

为了验证优化算法在数据倾斜场景下的稳定性，我们设计了三个自定义场景：

场景一：时间戳高度集中。
- 描述： 构造数据， $2\times 10^4$ 个用户，每个用户 $1800$ 个连续的活跃点。
- 目的： 测试算法在处理局部热点数据时的性能，验证块内和相邻块间计算逻辑的效率。
- 结果： 表现优异。由于数据高度局部化，分块算法和 BitSet 优化效果显著，网络传输量极小。基准实现内存超限，无法给出正确结果。

场景一数据生成的 SQL 语句
WITH
    users AS (SELECT posexplode(split(space(20000 - 1), ' ')) AS (seq, val)),
    timepoint AS (SELECT posexplode(split(space(1800 - 1), ' ')) AS (seq, val))
INSERT OVERWRITE TABLE concentrated_test_data
SELECT
    u.seq AS userid,
    t.seq AS active_time
FROM
    users u CROSS JOIN timepoint t;

场景二：时间戳稀疏且均匀分布。
- 描述： 构造数据， $10^5$ 个用户，每个用户 $144$ 个活跃点，分布在块号为 $0, 2,\cdots, 142$ 的非相邻块中，每个块内仅有最小和最大的两个端点。
- 目的： 测试算法在数据稀疏但跨度大的场景下的性能，检验 BitSet 优化的有效性。
- 结果： 性能稳定。BitSet 依然能够有效减少无效块信息的传输，虽然活跃块数量多，但总数据量仍在控制范围内。改进后的算法测量耗时 $5.64$ 秒，相比基准实现的 $5.52$ 秒，优化后的算法逻辑带来的额外开销仅有 $2.17 \%$ 。

场景二数据生成的 SQL 语句
WITH
    users AS (SELECT posexplode(split(space(100000 - 1), ' ')) AS (seq, val)),
    block AS (SELECT posexplode(split(space(144 - 1), ' ')) AS (seq, val))
INSERT OVERWRITE TABLE sparse_test_data
SELECT
    u.seq AS userid,
    (b.seq * 600) - (b.seq % 2) AS active_time
FROM
    users u CROSS JOIN block b;

场景三：巨量数据单点爆发。 模拟大量重复时间戳记录。
- 描述： 构造数据， $4\times 10^3$ 个用户，每个用户在某个时间点产生 $10^4$ 条重复记录。
- 目的： 测试 $\texttt{iterate}$ 方法的原始性能和更新逻辑的健壮性。
- 结果： 性能稳定。由于分块算法仅需维护每个块的值，海量重复数据并不会增加内存消耗， $\texttt{iterate}$ 方法内的计算（取模、除法、比较）极其轻量，处理效率高。基准实现内存超限，无法给出正确结果。

场景三数据生成的 SQL 语句
WITH
    users AS (SELECT posexplode(split(space(4000 - 1), ' ')) AS (seq, val)),
    duplicates AS (SELECT posexplode(split(space(10000 - 1), ' ')) AS (seq, val))
INSERT OVERWRITE TABLE burst_test_data
SELECT
    u.seq AS userid,
    u.seq % 600 AS active_time
FROM
    users u CROSS JOIN duplicates d;

自定义测试证明，本解法对各类数据倾斜场景均具有良好的适应性和稳定性。

关于未使用 JNI 的思考

在优化的最后阶段，我曾考虑使用 Java 本地接口（Java Native Interface，JNI）调用 C++ 代码来进一步提升计算性能，但最终放弃了此方案。

性能热点分析： 性能热点主要集中在 Map 阶段的数据读取（磁盘 I/O）和 $\texttt{iterate}$ 方法的调用。JNI 无法优化磁盘 I/O。
计算逻辑简单： $\texttt{iterate}$ 方法内部的核心计算仅包含整数的除法、取模以及比较，这些都是非常基础的运算。
JIT 编译器的威力： Java 的 HotSpot 虚拟机拥有强大的 JIT 编译器。对于 $\texttt{iterate}$ 这种频繁被调用的「热点方法」，JIT会将其编译为高度优化的本地机器码，其性能已经非常接近原生 C++ 代码。
JNI 的额外开销： 使用 JNI 会引入 Java 与 Native 代码之间的调用开销以及数据类型的转换开销。对于我们这样计算逻辑极其简单的场景，JNI 带来的开销很可能超过其带来的微小性能收益。

综上，在当前场景下，纯 Java 实现配合 JVM 的自动优化是更佳的选择。

总结

本报告提出并实现了一个高效计算用户在线时长的 Hive UDAF。通过采用 分块算法、稀疏数据传输优化 和 底层 I/O 优化，我们成功地将一个受内存、网络和计算性能限制的基准方案，改造成了一个高性能、高稳定性的解决方案。实践证明，深入理解业务数据特性并将其与算法设计相结合，是进行程序设计与优化的关键所在。

Apache Hive: GenericUDAFCaseStudy。 ↩︎
Jeffreys prior - Wikipedia。 ↩︎
BitSet (Java Platform SE 8)。 ↩︎
ByteBuffer (Java Platform SE 8)。 ↩︎
Randal E. Bryant 和 David R. O'Hallaron 在 Computer Systems: A Programmer's Perspective 中提出的一种性能测试方法。 ↩︎